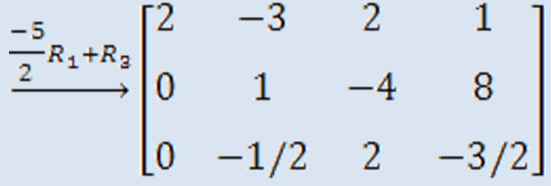Introducción
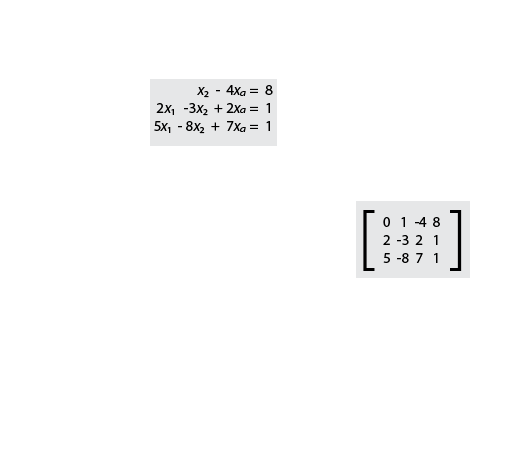
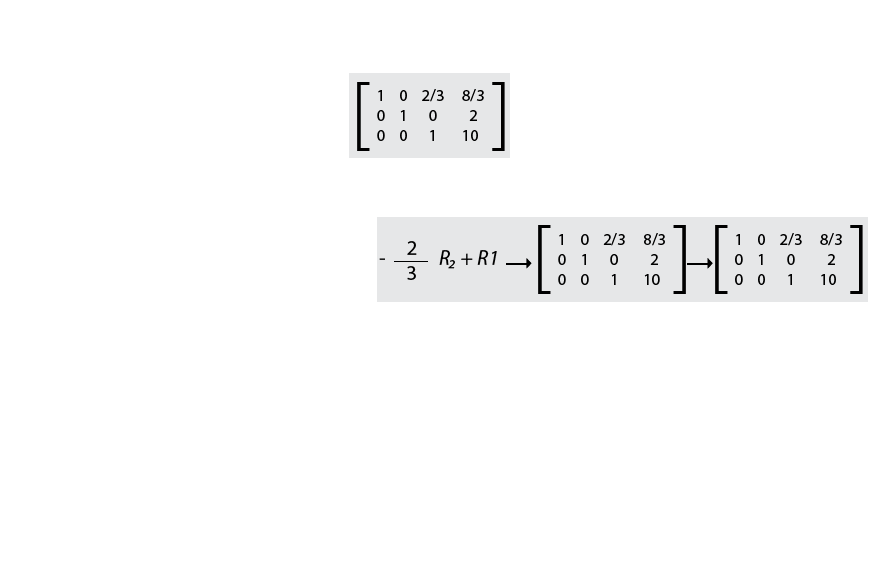
Hoy en día, existen muchas situaciones donde se requiere calcular valores para diferentes incógnitas que conforman los sistemas de ecuaciones lineales para satisfacer al sistema. Los sistemas de ecuaciones lineales se generan de acuerdo con las condiciones en que se dan las variables experimentales de un problema o proceso en estudio. Para la obtención de estos valores existen diversas metodologías, como el método de Gauss-Jordan, que permiten resolver el sistema propuesto; en esta variedad de recursos, el álgebra lineal tiene su mayor importancia.
Actualmente, las empresas requieren usar con frecuencia estos recursos debido a que se conforman internamente por diversas áreas de análisis donde se toman decisiones que forman parte de los planes de desarrollo y crecimiento de las organizaciones.

Medina, E. (2011). Empleado [fotografía]. Tomada de https://www.flickr.com/photos/65188416@N06/6028945721/